ATO Practice Statement Law Administration
PS LA 2006/8
| SUBJECT: | Remission of shortfall interest charge and general interest charge for shortfall periods |
|---|---|
| PURPOSE: | To provide guidelines on the remission of shortfall interest charge and general interest charge accrued during shortfall periods. |
This version is no longer current. Please follow this link to view the current version. |
-
This document incorporates revisions made since original publication. View its history and amending notices, if applicable.
FOI status: may be released
| TABLE OF CONTENTS | Paragraph |
|---|---|
| STATEMENT | |
| Introduction | |
| Application of this practice statement | |
| Exceptions | |
| GIC imposed on superannuation guarantee charge excluded from application of this practice statement | |
| GIC not accrued in the shortfall period excluded from application of this practice statement | |
| Imposition of interest charges | |
| Terms Used | |
| EXPLANATION | |
| Shortfall interest charge (2004-05 and later income years - income tax) | |
| GIC relating to the shortfall period (other taxes; 2003-04 and earlier years - income tax) | |
| Remission guidelines | |
| Remission of shortfall GIC to the SIC rate | |
| Partial remission for income tax - 2003-04 and earlier income years | |
| No remission of GIC to SIC rate for other taxes | |
| Circumstances where remission may be appropriate | |
| ATO delay | |
| Delay in commencing audit | |
| Expected audit completion date exceeded | |
| Unreasonable delay | |
| ATO delay in obtaining information from a third party | |
| Longer resolution times due to complexity of issue | |
| Large Corporate audits - delay based upon a reasonable time for completion of audits | |
| Cases involving fraud or evasion | |
| Taxpayer delay | |
| Delay is outside of taxpayer's control | |
| Taxpayer contributing to delay | |
| Taxpayer requests further time or delay | |
| Taxpayer delay due to an associate's or agent's delay | |
| Claims for legal professional privilege or access to professional advisors' working papers | |
| Unprompted voluntary disclosure | |
| Delay in processing requests for amendment | |
| Remission as an incentive for some compliance programs | |
| Advance payment of shortfall amount | |
| Tax shortfall offset by a related credit | |
| Income incorrectly apportioned between taxpayers | |
| Offset because of increase in pay as you go (PAYG) or other credits in amendment | |
| Costs of administration | |
| Reliance on ATO advice or general administrative practice | |
| Reliance on ATO Interpretative Decisions (ATO IDs) | |
| Reliance on subsequently overturned judicial interpretation | |
| Taxpayer could not have been aware of shortfall when lodging return | |
| Change or potential change in legislation with retrospective effect | |
| Income tax | |
| Indirect taxes | |
| Cases involving the use of the Commissioner's discretion to treat a particular document as a tax invoice or adjustment note | |
| Legislation | |
| Shortfall interest charge | |
| General interest charge | |
| Diagram of interest charges and shortfall periods |
|
This practice statement is issued under the authority of the Commissioner and must be read in conjunction with Law Administration Practice Statement PS LA 1998/1. It must be followed by Tax office staff unless doing so creates unintended consequences or is considered incorrect. Where this occurs Tax office staff must follow their business line's escalation process. |
STATEMENT
Introduction
1. Taxation interest charges are imposed:
- •
- to act as an incentive for payment of liabilities by their due date
- •
- to ensure that taxpayers who fail to fulfil their payment and return or statement obligations do not receive an advantage over those who meet their tax liabilities in full by the due date, and
- •
- to compensate the community for the impact of late payments.
2. To do this the taxation laws impose interest charges from the date a taxation liability should have originally been paid. These laws also provide the Commissioner with a discretionary power to remit interest charges where it is fair and reasonable to do so. For example, remission would occur where circumstances justify the Commonwealth bearing part or all of the cost of not having the funds at the proper time.
3. This practice statement outlines the Commissioner's remission guidelines in relation to interest charges:
- •
- that are imposed on shortfall amounts - that is an amount understated at the time of assessment, or notification, and
- •
- that accrue during the shortfall period - that is the period between when the shortfall would originally have been due for payment and when the shortfall is corrected, for example by giving a notice of an amended assessment.
4. These guidelines help decision makers make fair and consistent decisions on the remission of interest charges having regard to the facts of the matter and the individual circumstances of the taxpayer involved.
Application of this practice statement
5. This practice statement applies to interest charges that are imposed on shortfall amounts and accrue during the shortfall period. This is:
- •
- shortfall interest charge (SIC)
- •
- shortfall general interest charge (GIC) - that is, GIC accrued during the shortfall period on the shortfall amount, and
- •
- interest and GIC imposed under section 170AA of the Income Tax Assessment Act 1936 (ITAA 1936).
Exceptions
GIC imposed on superannuation guarantee charge excluded from application of this practice statement
6. This practice statement does not cover the remission policy in relation to shortfall GIC imposed on superannuation guarantee charge (SGC).
7. The SGC is an amount collected by the Commissioner on behalf of employees. It is payable by employers who have failed to provide the prescribed minimum level of superannuation support to their employees. GIC imposed on unpaid SGC is payable to the employees' superannuation funds to compensate the employees for loss of earnings that result when the SGC is paid late. Therefore it is not appropriate for the remission guidelines provided in this practice statement to apply to GIC imposed in respect of unpaid SGC.
8. Guidelines for remission of GIC imposed in respect of SGC are contained in the chapter 'General Interest Charge' in the ATO Receivables Policy.
GIC not accrued in the shortfall period excluded from application of this practice statement
9. Unless specifically provided for, this practice statement does not apply to GIC that is not shortfall GIC.
10. Guidelines for remission of GIC for late payment are contained in the chapter 'General Interest Charge' in the ATO Receivables Policy.
Imposition of interest charges
11. SIC and GIC are imposed by law. A summary of the legislation for SIC and GIC is in paragraphs 122 to 148 of this practice statement.
12. The following table details the main provisions relating to the imposition of interest charges during the shortfall period.
| Type of shortfall | Period to which shortfall relates: | Interest type | Legislative references |
|---|---|---|---|
| Income tax | 1999-2000 and earlier income years: | ||
| i. periods up to and including 30 June 1999 | interest | Sections 170AA and 214A of the ITAA 1936 | |
| ii. periods after 30 June 1999 | general interest charge | Section 170AA of the ITAA 1936 and Division 1 of Part IIA of the Taxation Administration Act 1953 (TAA) | |
| 2000-01 to 2003-04 income years | general interest charge | Section 5-1 of the ITAA 1997 and Division 1 of Part IIA of the TAA | |
| 2004-05 and later income years | shortfall interest charge | Division 280 of Schedule 1 to the TAA | |
| Petroleum resource rent tax (PRRT) | 2006-07 and later financial years | shortfall interest charge | Section 280-102 of Schedule 1 to the TAA |
| Minerals resource rent tax (MRRT) | 2012-13 and later MRRT years | shortfall interest charge | Section 280-101 of Schedule 1 to the TAA |
| Fringe benefits tax | amounts that are due to be paid on or after 1 July 1999 | general interest charge | Section 93 of the Fringe Benefits Tax Assessment Act 1986 and Division 1 of Part IIA of the TAA |
| Indirect taxes - goods and services taxes (GST), wine equalisation tax, (WET) and luxury car tax (LCT) | all periods | general interest charge | Section 40 and Division 1 of Part IIA of the TAA |
| Pay as you go withholding (PAYG(W)) | all periods | general interest charge | Section 16-80 of Schedule 1 and Division 1 of Part IIA of the TAA |
13. SIC generally applies in the same manner to MRRT and PRRT as it does for income tax. Therefore, while the practice statement refers only to income tax, the approach it outlines will be applied in a consistent manner in respect of MRRT and PRRT as well.
14. SIC and GIC apply regardless of whether or not the taxpayer is liable to any administrative penalty. Liability to SIC and GIC does not depend upon, nor imply, culpability on the part of the taxpayer.
Terms used
15. For the purposes of this practice statement some terms are defined in the following paragraphs.
16. Audit Cycle Timeframes - The time that it is expected a particular type of audit should take from commencement to completion. The amount of time will vary depending on the type of activity being audited, the tax type and market.
17. Base interest rate or base rate - A rate set by law which is used as a base for calculating SIC and GIC. For each day in a particular quarter of the year, the base interest rate equals the monthly average yield of 90 day Bank Accepted Bills for a prescribed previous month. For example, for the quarter 1 January to 31 March, the base interest rate is the monthly average yield of 90 day Bank Accepted Bills for the preceding November (subsection 8AAD(2) of the TAA).
18. Commencement of audit - The first day of the initiate phase of the audit in the case management system. This date will generally be before the taxpayer is advised of the audit.
19. Completion of audit - The date the notice of assessment (or the equivalent notification of the adjustment for other taxes) which includes the shortfall amount issues.
20. Expected audit completion date - When notifying a taxpayer of the intention to audit, the Australian Taxation Office (ATO) will generally provide an expected audit completion date in that notice. This date will be determined by applying a pre-determined audit cycle timeframe to the commencement of the audit to calculate the expected completion date. The cycle timeframe will be different for different taxes, products and markets. The cycle timeframes will be:
- •
- for Large Corporate audits commencing on or after 1 July 2005 - the time notified at the commencement of the audit or 2 years, whichever is the shorter period, and
- •
- for all other audits commencing on or after 1 July 2006 - as published on the ATO intranet.
21. GIC rate - The GIC rate is the base interest rate plus an uplift factor of seven percentage points. This rate including uplift factor is imposed by law (subsection 8AAD(1) of the TAA).[1]
22. Interest Charges - includes shortfall interest charge (SIC), shortfall general interest charge and interest imposed under section 170AA of the ITAA 1936. Section 170AA interest relates to periods up to 30 June 1999.
23. Shortfall amount - the difference between an amount of tax payable, as reported in a statement or included in an assessment, and the amount of tax payable calculated by the Commissioner to correct an understatement and subsequently included in an assessment or other notification.
24. Shortfall GIC - GIC which relates to the shortfall period. It is payable in respect of:
- •
- amended income tax liabilities for the 2000-01 to 2003-04 income years, and
- •
- shortfalls raised for other tax-related liabilities.
25. Shortfall period - The shortfall period starts on the day the tax debt was due for payment or would have been due for payment had the shortfall been correctly reported and ceases on the day before the Commissioner gives the taxpayer a notice of assessment which includes the shortfall amount (or an equivalent notification for taxes other than income tax).
Example: Taxpayer has an income tax liability for the 2004-05 income tax assessment of $500 due for payment on 21 November 2005. The taxpayer requests amendment of the assessment on 1 March 2006. An amended notice of assessment is given to the taxpayer on 20 March 2006 increasing the tax payable by $125 to $625. The shortfall amount is $125 and the shortfall period is from 21 November 2005 to 19 March 2006.
Example: Taxpayer has a 2003-04 income tax assessment of $15,000 due on 1 December 2004. Following an audit by the ATO an amended notice of assessment is given to the taxpayer on 1 June 2006 increasing the tax payable by $3,000 to $18,000. The shortfall amount is $3,000 and the shortfall period is 1 December 2004 to 31 May 2006.
Example: Taxpayer lodges an activity statement on 10 April 2006 reporting a GST liability of $20,000 for the month of February 2006. The debt was due on 21 March 2006. The taxpayer advises on 25 May 2006 that the GST liability was understated by $8,720. The activity statement is adjusted on 25 May 2006 and a notice is given to the taxpayer the following day. The shortfall period is from 21 March 2006 until 25 May 2006.
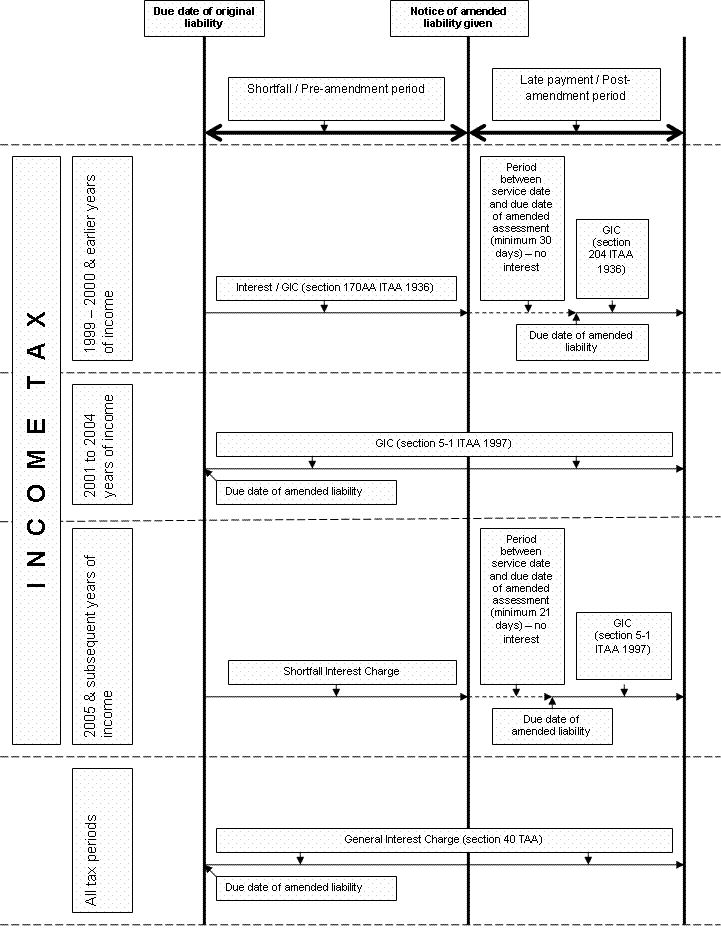
26. A diagram illustrating when interest charges accrue in shortfall periods can be found at paragraph 149 of this practice statement.
27. SIC rate - The SIC rate is the base interest rate plus an uplift factor of three percentage points. This rate including the uplift factor is imposed by law (subsection 280-105(2) of Schedule 1 to the TAA.)[2]
EXPLANATION
Shortfall interest charge (2004-05 and later income years - income tax)
28. An interest charge at a lower rate than GIC has been introduced for shortfall amounts for income tax amendments for the 2004-05 and later income years. This lower interest charge is known as the shortfall interest charge (SIC).
29. This lower rate was introduced because taxpayers who are genuinely unaware of the shortfall may be unable to take any steps to reduce their exposure to GIC.
30. The principal object of the SIC is to neutralise benefits that taxpayers could otherwise receive from shortfalls of income tax, so that they do not receive an advantage over those who pay the tax properly owing at the appropriate time.
GIC relating to the shortfall period (other taxes; 2003-04 and earlier years - income tax)
31. As SIC only applies to amended income tax liabilities for the 2004-05 and later income years, shortfalls in respect of other taxes, and shortfalls that relate to income tax liabilities for income years 2000-01 to 2003-04 will continue to attract GIC from the original due date for payment.
32. Income tax amendments for the 1999-2000 and earlier income years attract interest in the shortfall period under section 170AA of the ITAA 1936. For shortfall periods from 1 July 1999 this interest is imposed as GIC. A reference in this practice statement relating to the remission of shortfall GIC will apply equally to remission of interest and general interest charge imposed under section 170AA of the ITAA 1936.
Remission guidelines
33. SIC and GIC are imposed by the law in all relevant shortfall cases. Interest charges in the shortfall period are intended to reconcile the position of those taxpayers whose liabilities are amended and those who paid the correct amount of tax under the original assessment.
34. The Commissioner has a responsibility to recover unpaid interest charges like any other tax-related liability.
35. The Commissioner may remit all or part of SIC or shortfall GIC where the Commissioner considers it fair and reasonable to do so. In relation to the remission of SIC, paragraph 280-160(2)(b) of Schedule 1 to the TAA states that the Commissioner must have regard to the principle that remission should occur where the circumstances justify the Commonwealth bearing part or all of the cost of delayed payments.
36. The extent of the remission must take into account the individual circumstances of a case. In the examples below guidance is provided on the extent of the remission. In a number of examples remission of the interest charge to the base rate is considered to be appropriate. However, the extent of the remission in any case must have regard to the particular circumstances and the extent to which factors beyond the taxpayer's control were responsible for the size and duration of the shortfall. In some cases, circumstances may justify remission to below the base rate, including full remission.
37. Remission can be requested by the taxpayer or initiated by the Commissioner.
38. In all cases where there is a SIC and/or GIC liability tax officers should consider remission where circumstances justifying remission are readily apparent. Such circumstances may not be readily apparent in automatic amendment and data matching cases.
39. Taxpayers can request remission of SIC or GIC at any time. In addition to the right to formally object in certain circumstances as outlined in paragraph 137 of this practice statement, a taxpayer is not prevented from making their own representations addressing similar or different grounds after the Commissioner has considered remission.
40. The taxpayer's application should be in writing, describing their circumstances, and the grounds on which the taxpayer relies for remission. The Commissioner will consider all of the factors put forward by a taxpayer in a request for remission and any other factors that may be relevant.
41. SIC and GIC (interest charges) are intended to restore a fair balance between taxpayers, ensuring that taxpayers who have paid tax on time are not disadvantaged relative to those who had the benefit of the tax shortfall until the amended assessment. This should be contrasted with shortfall penalties, which relate to the taxpayer's behaviour leading up to the shortfall and the degree of cooperation or obstruction demonstrated by the taxpayer in correcting the shortfall. Accordingly, it does not necessarily follow that a reduction or remission in shortfall penalty will automatically mean a reduction or remission of the interest charge.
Remission of shortfall GIC to the SIC rate
Partial remission for income tax - 2003-04 and earlier income years
42. As SIC only applies to income tax shortfalls for the 2004-05 and later income years, the higher GIC applies in relation to income tax shortfalls for earlier years.
43. The extension of the SIC regime to earlier income years would have resulted in unequal treatment of assessments for the same year. For example, those taxpayers whose assessments were amended before the introduction of the SIC would have had the higher GIC imposed. On the other hand continuing to apply the higher GIC rate from 1 July 2005 (when the SIC regime broadly commenced after the end of the 2004-05 income year) could be seen to be unfair and at odds with Parliament's decision that the GIC rate was excessive during a shortfall period.
44. Having regard to these circumstances it is considered fair and reasonable that shortfall GIC generally be remitted to the SIC rate for the period from 1 July 2005 to the day before the amended assessment is issued.
Example: An amendment to Service Pty Ltd's 2002-03 income tax assessment issues on 15 March 2006. Shortfall GIC accrues from 1 December 2003.
The GIC would be remitted by 4 percentage points for the period from 1 July 2005 to 14 March 2006. This will equate the GIC for that period to the SIC rate. Further remission during the shortfall period may occur if some other circumstance exists which would warrant further remission in accordance with the guidelines contained in this practice statement.
No remission of GIC to SIC rate for other taxes
45. As the SIC regime only applies to income tax shortfalls the above considerations do not apply to GIC imposed in respect of other shortfall amounts.
46. The remission of GIC that accrues during a shortfall period for other tax liabilities will be considered in accordance with the guidelines outlined in this practice statement.
Circumstances where remission may be appropriate
47. The following are examples of circumstances in which remission may be appropriate. The considerations set out are not exhaustive and are not intended to limit the Commissioner in his discretion to remit interest charges when it is fair and reasonable to do so.
ATO delay
48. The Commissioner may remit where there has been delay or a longer than expected time taken in issuing an amended assessment.
Delay in commencing audit
49. The allocation of the ATO's resources necessarily means that not all audits can start immediately following self-assessment by a taxpayer.
50. As a rule of thumb it could be expected that an audit will commence within a period equivalent to 50% of the relevant period of review. However cases may commence at a later time, for example, where information is provided to the ATO from an external source at a later time. Where there has been an unreasonable delay in the ATO allocating a case for audit, remission of interest charges to the base rate may be appropriate for the period of such delay.
51. Where there is an unlimited period to amend an assessment it would normally be appropriate when considering remission to adopt the standard period of review applicable to the year being adjusted.
Expected audit completion date exceeded
52. Cycle timeframes have been set for specific types of audit activity. They will differ according to the expected type of activities being audited, the tax type and the market.
53. When notifying a taxpayer of the intention to audit, the ATO will generally provide an expected audit completion date in that notice. This date will be determined by applying a pre-determined cycle timeframe, or some lesser time having regard to the circumstances of the case, and calculating the expected completion date.[3]
54. Providing the scope of the audit remains much the same throughout the course of the audit and the taxpayer does not unreasonably delay or obstruct the progress of the audit, interest charges may be remitted to the base rate for the period the audit goes beyond the expected completion date.
Example: The GST record keeping audit cycle timeframe is 30 days. If the GST audit takes 40 days, remission to base rate for the final 10 days may be appropriate.
Example: A 'GST specific audit - phone' audit of a taxpayer's business is commenced by a GST office auditor on 23 June 2006. The audit cycle timeframe is 40 days. However, on 26 July 2006, 33 days into the audit, it becomes apparent to the auditor that there are several risks involved in the case and that the work is more appropriately considered a GST micro comprehensive audit with a 225 days cycle timeframe. The case is transferred to a GST field auditor for completion on 27 July 2006. The cycle timeframe will extend to 225 days from 23 June 2006.
55. This ground for possible remission based on the expected audit completion date applies to audits which started on or after 1 July 2006 when these cycle times were first published, other than for Large Corporate audits where an earlier announcement was made: see paragraphs 66 to 68 of this practice statement. For audits commenced before that date, remission will occur on a case by case basis using the principles outlined in this practice statement.
56. Remission for periods during the cycle timeframe period may still occur if there are other grounds for remission, as set out in other sections of this practice statement. Where remission relating to a period during the audit cycle timeframe is granted this may need to be taken into account when determining the extent of remission for the period beyond the expected completion date.
Example: An audit commences on 1 February 2006 and has an expected audit completion date of 30 June 2006. The audit is not completed until 30 September 2006. Due to an unreasonable ATO delay full remission is granted for the period 1 April 2006 to 31 May 2006. Normally remission to the base rate would be applicable for the three month period which exceeded the expected audit completion date - 1 July 2006 to 30 September 2006. However as full remission has already been granted for a period of two months remission to the base rate is only appropriate for one month - 1 September 2006 to 30 September 2006.
57. Where an audit case is completed beyond the expected audit completion date, the case authorising officer must undertake a full review of the reasons for the delay to determine whether further remission grounds apply.
Unreasonable delay
58. The completion of an audit within the cycle timeframe and before the expected audit completion date does not preclude other grounds for remission. There may have been unreasonable delays or periods of inactivity outside the control of the taxpayer during the audit that warrant remission of interest charges.
59. As a general rule where there has been no action on a case for 30 days or more and it was possible for the case to progress during that time, full remission of the interest charges for the period of unreasonable delay would be warranted.
Example: An audit of John's 2004-05 income tax affairs commences on 1 July 2006 with an expected audit completion date of 27 November 2006.
On 2 September 2006 the auditor seeks more information from the taxpayer and provides a response date of 30 September 2006.
By that date all the necessary information to determine a shortfall has been gathered and interviews have occurred.
On 2 October 2006 the auditor submits his final audit report to his team leader to authorise the case result. The team leader does not review the submission until 15 November 2006 and then authorises the result without change. The amendment issues on 20 November 2006.
Assuming there are no other circumstances relevant to the remission of interest charges full remission of interest charges will be appropriate from 2 November 2006 to 15 November 2006 (the total period of inactivity which exceeds 30 days).
60. The cycle timeframe is set to enable ATO auditors to complete the audit as well as carry out other appropriate duties that may occur concurrently. If there are up to 30 days where the auditor did not work on the audit and the audit is completed within the benchmark, generally ordinary delays of this nature would not of themselves warrant remission.
ATO delay in obtaining information from a third party
61. Where the ATO or the taxpayer experiences delay in obtaining information from a third party and this information is not otherwise available to the taxpayer remission to the base rate is warranted for the period of the delay.
62. However where the ATO experiences delay in obtaining information because the taxpayer has been unwilling or unable to supply information that they should have, or that they are readily able to obtain, remission will generally not be granted for the delay.
Longer resolution times due to complexity of issues
63. Where there is complexity involved in the issues underlying a shortfall, it may take some time to come to a view as to the proper operation of the law. So there may be a hiatus between the commencement of the audit and the amendment of the assessment.
64. The referral of a complex matter to a specialist forum or network for resolution does not in itself constitute a delay that would warrant remission of interest charges. The cycle timeframes for the audit generally factor in issues of complexity, and the time taken for their resolution.
65. However, remission to the base rate would be warranted where the resolution of the issue took longer than would be reasonably expected and resulted in the case exceeding the expected audit completion date.
Large Corporate audits - delay based upon a reasonable time for completion of audit
66. Shortfall GIC and SIC will be remitted to the base interest rate for the period that a Large Corporate audit extends beyond two years.
67. Only in exceptional cases involving blatant obstruction, delays or obfuscation will this remission not apply. Such cases will need to be agreed to by the Deputy Commissioner of the ATO's Large Business area following discussion with executives of the relevant corporation.
68. This approach will apply for audits commenced on or after 1 July 2005. For audits commenced prior to that date remission based on delay will continue to be considered on a case by case basis using the principles outlined in this practice statement.
69. This '2 year' policy will not apply to transfer pricing audits subject to a Mutual Agreement Procedure which are covered by other arrangements in the ATO Receivables Policy and Taxation Ruling TR 2000/16. Otherwise the principles in this practice statement apply to transfer pricing cases.
70. This '2 year' policy does not preclude remission being granted for periods prior to the commencement of the audit or the period within two years from commencement of the audit, if particular delays occur which might warrant remission. The factors outlined in other sections of this practice statement may also need to be considered in some cases.
Cases involving fraud or evasion
71. Where a case involves fraud or evasion remission would not normally be granted notwithstanding that there may have been some delay attributable to the ATO or the expected audit completion date is exceeded. Remission in these cases would still be considered on a case by case basis, but having due regard to the circumstances giving rise to the shortfall.
72. In such cases, the taxpayer would have been aware of the potential tax shortfall and could have taken steps to reduce their exposure to interest charges.
Taxpayer delay
Delay is outside of taxpayer's control
73. Full remission for the period of the delay may be appropriate where the taxpayer can demonstrate the delay in supplying information or documents for the audit was directly attributable to:
- •
- natural disasters (flood, fire, drought, earthquake and the like)
- •
- other disasters that may have, or have had, a significant impact on the taxpayer or region, or
- •
- the serious illness of the taxpayer or key personnel where there is no other person that could have mitigated the length of the delay.
74. Remission is not usually appropriate where the reasons for the delay are within the taxpayer's control. This may include delays where the taxpayer takes an extended vacation after the commencement of the audit. However if the taxpayer had booked prior to the commencement of the audit or needs to travel overseas for business purposes those circumstances could be taken into account in considering remission to the base rate.
Taxpayer contributing to delay
75. Where the taxpayer unreasonably delays, obstructs or obfuscates the progress of an audit, and the audit is completed beyond the expected audit completion date, remission will not generally be warranted. Examples of such conduct include:
- •
- repeated failure by the taxpayer to keep appointments or supply information, or
- •
- repeated failure by the taxpayer to respond adequately to reasonable requests for information. This will include excessive or repeated delays in responding, not replying to the request for information, giving information that is not relevant or does not address all the issues in the request or supplying inadequate information.
Example: The company Tenor Pty Ltd claimed losses in its 2003-04 income tax return. The auditor asks for a copy of the loss schedule and other information, which should have been prepared in order to lodge the return, to be provided within 28 days. Not having received the information, on the 30th day following the request the auditor rings the company and four days later the documents are faxed to the ATO. In this instance the time taken to collect the information would not be considered a delay attributable to the taxpayer (or the ATO).
However, Soprano Pty Ltd when asked for the same information on the 30th day following the request advised that it had overlooked the enquiry, and would deal with it quickly. Fourteen days later the auditor contacted the company and was unable to speak with anyone who knew about the request. The auditor then sent a further request for information to the company. At the end of the 28 day period after the second request the auditor received a copy of the profit and loss statement for the 2003-04 year but not the loss schedule and the remaining information was only partially provided. This would be a delay due to the taxpayer's conduct, unless the taxpayer could adequately explain the delay.
76. A decision not to remit because of the taxpayer's behaviour must be agreed to by a Senior Executive Service officer.
Taxpayer requests further time or delay
77. Taxpayers may request a deferment of action during an audit, for example, by requesting significant further time to supply information. Interest charges may be remitted to the base rate for the period where the taxpayer requests extra time where the gathering of the information with all due diligence by the taxpayer necessitates that extra time.
Example: The taxpayer needs 6 weeks additional time to gather and supply information. The auditor accepts this and allows the time requested. Interest charges would be remitted to the base rate for the period of delay.
78. However where, for example, at the request of the management of a taxpayer group, amended assessments are deferred until the completion of the audit of the group, interest charges would not normally be remitted for the period of that particular delay.
Taxpayer delay due to an associate's or agent's delay
79. As stated at paragraph 61 of this practice statement, where a delay in establishing a shortfall is due to a third party, remission of interest charges to the base interest rate may be warranted for the period of delay. However where the third party is an associate of the taxpayer or not dealing at arms length with the taxpayer, remission under this ground will not usually be given unless the delay is reasonable and beyond anyone's control.
80. A delay caused by a taxpayer's tax agent or other representative will generally be considered to be a delay attributable to the taxpayer. It then needs to be considered whether the delay is reasonable and beyond anyone's control.
Example: A tax agent is unable to provide the information requested for several weeks due to their commitments under their tax agent lodgment program and other compliance obligations. This delay is attributable to the taxpayer. However if the delay is reasonable interest charges may be remitted to the base rate.
Claims for legal professional privilege or access to professional advisors' working papers
81. Taxpayers may seek advice from professional advisors on issues such as the application of legal professional privilege to certain documents or the right of access to professional accounting advisors' working papers. Such claims form part of the normal dealings of a taxpayer with the ATO. Should reasonable claims lead to the case being completed beyond the expected audit completion date, then interest charges would generally be remitted to the base rate for the period that goes beyond that completion date.
Unprompted voluntary disclosure
82. Where a taxpayer makes a voluntary disclosure of a shortfall (often referred to as a self-amendment), the disclosure itself is not a ground for routine remission.
83. A taxpayer who has self-assessed incorrectly, even if reasonable care was exercised, should not end up in a more beneficial position than a taxpayer who has self-assessed and paid correctly.
84. However, there may be some cases where the circumstances surrounding the voluntary disclosure will make it fair and reasonable to remit interest charges. Where remission on the basis of a voluntary disclosure is considered appropriate it will generally be to the base rate.
85. Any remission of interest charges on the basis of a voluntary disclosure should have regard to the following:
- •
- the timeliness of the disclosure after the error was first detected
- •
- whether the disclosure was made before notification of the commencement of an audit or before the notification or publication of a ATO initiative which may have led to the discovery of the shortfall by the Commissioner
- •
- whether the Commonwealth in any way contributed to the taxpayer taking their original position
- •
- the size of the shortfall, either in monetary terms or in relation to the totality of the taxpayer's affairs, and
- •
- the taxpayer's compliance history, including the number of times a taxpayer has had to disclose shortfalls following an initial self-assessment of liability.
Example: Big Co. Ltd. has an internal assurance practice of reviewing its previous income tax return in preparation for lodging their next return. As part of this process Big Co. Ltd identifies a shortfall and immediately lodges an amendment request. As no audit activity was being undertaken or planned by the ATO in respect of the issue or income year remission of interest charges to the base rate would be appropriate in this case.
86. The ATO may adopt specific interest rate remission incentives to encourage voluntary disclosure in particular compliance programs. This is dealt with further at paragraph 89 of this practice statement.
Delay in processing requests for amendment by taxpayers
87. Where a taxpayer self-amends or makes a voluntary disclosure, that is, voluntarily seeks to correct an error in an earlier return or statement, the ATO has published service standards for processing amendments or adjustments.[4]
88. In order to amend the assessment the ATO may need further information to establish the correct tax file number, the correct amounts and some details of why the amendment is occurring. If this information is not supplied the taxpayer is generally contacted. Where or once the ATO has all information needed to process the amendment or adjustment, the Commissioner will generally remit in full the interest charges for any delay beyond the published standard.
Example: Raji lodges a 2004-05 amendment request on 1 August 2006. All the information is included in the request. This amendment is lodged in writing (not via ELS), and should be processed within 56 days of receipt, that is by 26 September 2006. Because of a backlog in work, the amended notice of assessment is not given to the taxpayer until 5 October 2006. Remission in full should occur for the period from 27 September 2006 to 4 October 2006.
Remission as an incentive for some compliance programs
89. Specific interest rate remission guidelines could be adopted by the ATO as part of particular compliance programs or to ensure consistency of treatment with similar situations that have already been determined and announced. However, this does not preclude other outcomes consistent with these guidelines having regard to the facts and circumstances of the particular case.
Advance payment of shortfall amount
90. Paying the shortfall amount before the issue of an amended assessment does not stop SIC accruing.[5] That is, the SIC is calculated to the day before the amended assessment is given to the taxpayer and on the total shortfall regardless of whether the shortfall amount has been paid in full or in part before that date. However, any benefit a taxpayer may have because of non-payment ceases when full payment is made.
91. The SIC for the period after full payment will be remitted in full, subject to paragraph 92 of this practice statement. Where a part payment of the shortfall has been made, a partial remission reflecting the portion of the shortfall paid will be given for the post-payment period.
92. To ensure a revenue neutral position for the period following payment the extent of any remission will take into account any interest the taxpayer may be entitled to under the Taxation (Interest on Overpayments and Early Payments) Act 1983, in particular, entitlement to interest on early payment (IEP) under Part IIA of that Act. For further information refer to the ATO Receivables Policy chapter 'Interest on Early Payments'.
93. SIC remission from the date of payment should be reduced by an amount equal to the IEP entitlement that accrues between the date of payment and the day before the amended notice of assessment is given to the taxpayer. Any IEP entitlement relating to the payment period from the date the notice is given to the taxpayer to the due date of the amended assessment does not affect the level of remission.
Example: After discovering a shortfall, on 1 July 2006 Compliant Pty Ltd lodges an amendment request and on the same date makes payment of $1,000 - the tax payable on the shortfall. An amended assessment for the $1,000 tax shortfall is given to the taxpayer on 1 August 2006 and is due for payment on 22 August 2006.
Under the law SIC on the $1,000 shortfall is payable for the period from 1 December 2005, the due date of Compliant Pty Ltd's original assessment, to 31 July 2006, the day before the notice of amended assessment is given to the taxpayer.
However as payment of the shortfall was made on 1 July 2006, remission of SIC for the period 1 July 2006 to 31 July 2006 is justified.
As Compliant Pty Ltd is entitled to interest on early payment for the period from 1 July 2006 (the day the early payment was made) to 22 August 2006 (the due date of the amended assessment) the amount of the SIC remission would be determined as follows:
SIC for period 1 July 2006 to 31 July 2006 less interest on early payment entitlement for period 1 July 2006 to 31 July 2006.
Tax shortfall offset by a related credit
94. Where the tax shortfall on which the SIC was imposed is offset by a related credit or overpayment, for example on an associated taxpayer's account, it may be fair and reasonable to remit the interest charges to the base rate.
Income incorrectly apportioned between taxpayers
95. Where income has been incorrectly apportioned between taxpayers and one taxpayer has paid the tax on that income, some remission may be appropriate when the amendment to correct the error occurs.
96. Any remission will be for the period in which the revenue has not been disadvantaged. For instance, the period for which interest charges are to be remitted would only relate to the period since payment of that other liability was received and to the extent of the shortfall or payment. Some of the factors to take into consideration in deciding whether the revenue has not been disadvantaged include each taxpayer's marginal tax rate and any entitlement to interest under the Taxation (Interest on Overpayments and Early Payments) Act 1983. Remission in these cases would be to the extent of neutralising the disadvantage (if any) to the revenue.
Example: John and Mary have a joint bank account and in the 2006 income year receive $5,200 interest. Initially John declared all the interest in his return. Both John and Mary's assessments are due on 21 November 2006. They have the same marginal rate of tax.
Subsequently both John and Mary sought to have their 2006 assessments amended; John by reducing his taxable income by $2,600 and Mary by increasing hers by $2,600. The amended notices of assessment issued on 1 September 2007. Mary's tax shortfall is $819 ($2,600 ? 31.5%, 31.5% being Mary's marginal tax rate of 30% plus Medicare levy of 1.5%).
Mary would be liable to SIC on $819 for the period from 21 November 2006, the due date of her original assessment, to 31 August 2007, the day before notice is given of the amended assessment. Assuming a SIC rate of 8.6% per annum during this period, SIC of $56.67 will be imposed
If John had paid his original assessment on 21 November 2006 then some remission of Mary's SIC is warranted for the period from when John had made payment. John is entitled to interest for overpayment of $36.47 which in this example would be at a rate of 5.6% per annum. He is entitled from the date of payment to the day before the notice is given to him. That is, from 21 November 2006 to 31 August 2007. Mary's SIC would be remitted by $20.20 and SIC of $36.47 would remain payable with the amended assessment.
If on the other hand John had not paid his original assessment then no remission of Mary's SIC is warranted as the Commonwealth will continue to bear the $819 shortfall until Mary pays that amount.
Offset because of increase in pay as you go (PAYG) withholding or other credits in amendment
97. Where an amended assessment is made SIC or shortfall GIC is calculated on the additional amount of income tax that is properly payable. In determining the additional amount of income tax payable certain credits, for example PAYG withholding credits, are excluded from the calculation as at law they are not an element of the assessment.
98. However where an entitlement to an additional amount of credit is also notified with the amended assessment full remission of SIC to the extent of the additional credit is appropriate.
Example: After the issue of her 2006 assessment Betty received a payment summary from a former employer. The payment summary showed $5,000 income and $1,200 PAYG withholding credits. She had not declared this income or the credits in her 2006 return.
Betty requested an amendment of her assessment to reflect the additional income. The additional tax payable under the amended assessment was $1,575 but after the PAYG withholding credit of $1,200 was applied against this amount Betty was required to pay $375.
As SIC is calculated on the additional tax payable (shortfall amount) of $1,575 remission equivalent to the amount of SIC calculated on $1,200 for the entire shortfall period will be given. That is, after remission only the SIC on $375 will remain for the shortfall period.
Costs of administration
99. The Commissioner may remit amounts because the amount of the interest charge is minimal. For example, the imposition of an amount of SIC or GIC below a small threshold amount will result in remission as part of the ATO's automated processes.
Reliance on ATO advice or general administrative practice
100. A taxpayer will be protected under the law from the GIC or the SIC that relates to a shortfall if:
- •
- the taxpayer relies in good faith on advice given to them or their agent by the Commissioner or a statement in a publication approved in writing by the Commissioner, unless the advice or the statement or publication is labelled as non-binding, or
- •
- the taxpayer relies in good faith on the Commissioner's general administrative practice.
101. This statutory protection applies:
- •
- to interest charges under a relevant provision (listed below at paragraph 104 of this practice statement), and
- •
- if, on or after 1 January 2006, the taxpayer relied upon the advice, statement or general administrative practice.
102. In these circumstances, interest charges are not imposed for the shortfall period (subsection 361-5(1) of Schedule 1 to the TAA).
103. The protection relating to the interest charges does not apply to amounts which accrue more than 21 days after the Commissioner notifies the taxpayer of the correct position (subsection 361-5(2) of Schedule 1 to the TAA).
104. A 'relevant provision' (section 357-55 of Schedule 1 to the TAA) is a provision about any of the following:
- •
- income tax
- •
- Medicare levy
- •
- fringe benefits tax
- •
- franking tax
- •
- withholding tax
- •
- mining withholding tax
- •
- petroleum resource rent tax
- •
- minerals resource rent tax
- •
- indirect tax
- •
- excise duty
- •
- the administration or collection of those taxes, levies and duties
- •
- a grant or benefit mentioned in section 8 of the Product Grants and Benefits Administration Act 2000, or the administration or payment of such a grant or benefit
- •
- a net fuel amount, or the administration, collection or payment of a net fuel amount
- •
- a net amount, or the administration, collection or payment of a net amount, or
- •
- a wine tax credit, or the administration or payment of a wine tax credit.
105. A general administrative practice will usually be established by the ATO having communicated consistently to a wide range of taxpayers on a particular issue. A general administrative practice is usually adopted for the efficient administration of the taxation system and would generally be documented in products such as:
- •
- Law Administration Practice Statements
- •
- General Administration Law Administration Practice Statements, and
- •
- ATO policy documents, such as the ATO Receivables Policy.
106. Not all precedential material (such as ATO Interpretative Decisions (ATO IDs) and draft public rulings) indicates a general administrative practice. An ATO ID or draft public ruling will only be accepted by the ATO as representing general administrative practice where the view contained therein is supported by other evidence of a long term and consistent pattern of active ATO treatment of the issue consistent with the view expressed in the precedential material.
107. Section 361-5 of Schedule 1 to the TAA does not apply where a shortfall arises under a provision that is not a relevant provision or a shortfall amount is caused by reliance before 1 January 2006 on non-ruling advice, a statement in a publication approved in writing by the Commissioner or a general administrative practice.
108. A shortfall that falls outside section 361-5 may arise as a result of a taxpayer having in good faith followed ATO advice, a statement in a publication approved in writing by the Commissioner or a general administrative practice. Where that advice, statement or practice is incorrect or misleading and the taxpayer makes a mistake as a result, any interest charges that apply in the period up until 21 days after the Commissioner notifies the correct position to the taxpayer will be remitted in full.
Reliance on ATO Interpretative Decisions (ATO IDs)
109. ATO IDs are published as precedential ATO views for tax officers. Although ATO IDs are publications approved in writing by the Commissioner, they are not published as a form of advice. They are made available to the public on the ATO Legal Database as a guide only, for purposes of transparency and to meet Freedom of Information requirements because they may be used by an officer in making another decision. Nevertheless, where a tax shortfall that falls within section 361-5 arises as a result of a taxpayer having reasonably relied in good faith on an ATO ID (a publication approved in writing by the Commissioner) by applying it to their own circumstances (which are not materially different from those described in the ATO ID) and that ATO ID is later found to be incorrect, interest charges are not imposed for the period up until 21 days after the Commissioner notifies the taxpayer of the correct position.
110. A shortfall amount that falls outside section 361-5 (for example, the ATO ID is about an indirect tax provision or reliance on the ATO ID was before 1 January 2006) may arise as a result of a taxpayer having reasonably relied in good faith on an ATO ID by applying it to their own circumstances (which are not materially different from those described in the ATO ID) and that ATO ID is later found to be incorrect. In these situations, interest charges for the period up until 21 days after the Commissioner notifies the taxpayer of the correct position will be remitted in full.
Reliance on subsequently overturned judicial interpretation
111. There will be situations where a taxpayer prepares a return or activity statement in a particular way, having regard to a decision of an independent tribunal or a court and, subsequent to lodgment of the return or activity statement, a court of higher authority overturns that decision, resulting in an unexpected tax shortfall.
112. Interest charges will be remitted in full in this situation, provided that:
- •
- the court or tribunal decision relied upon in the preparation of the return clearly applied to the taxpayer's circumstances, and
- •
- appropriate amendment requests are lodged within a reasonable time after the date of the final court decision. (There may be some circumstances where the ATO will initiate amendments).
113. If the taxpayer did not lodge an amendment request within a reasonable time, then there would not generally be any remission of interest charges which accrue from the date of the final court decision.
Taxpayer could not have been aware of shortfall when lodging return
114. A tax shortfall may arise because when the taxpayer lodged their original return or activity statement, they did not know and could not have known that a shortfall would arise. This would occur where the return or activity statement is correct and it is only future events that trigger the need to adjust a liability. Examples of this include (this list is not exhaustive):
- •
- Where a taxpayer becomes entitled to a receipt of compensation in a particular year, which may in some circumstances trigger an adjustment to capital proceeds and affect capital gains or losses in an earlier year's return, even though the taxpayer does not actually receive the compensation until a later date. Law Administration Practice Statement PS LA 2004/5(GA) gives an example of this situation.
- •
- Where member companies of a consolidated group are affected by the requirements of section 701-70 of the Income Tax Assessment Act 1997, when the head company makes an election to consolidate after the member company has already lodged its income tax return for the year.
115. Each case must be examined on its merits. In such situations it may be appropriate to grant full remission of interest charges related to the shortfall, usually on the condition that appropriate amendment requests are lodged within a reasonable time after the need to amend arises - this would be seen as fair and reasonable.
116. Remission on this basis only applies where the factual circumstances are such that the taxpayer could not have known about the shortfall when lodging their return. It does not apply to taxpayers who, for example, mistakenly believed the law operated in a way such that a shortfall would not arise.
Change or potential change in legislation with retrospective effect
Income tax
117. Where a tax shortfall arises as a result of a change in legislation which has retrospective effect, interest charges will be remitted in full for taxpayers who actively seek to amend their returns within a reasonable time after the enactment of the new law that increases their tax liability. If the taxpayer does not lodge an amendment request within a reasonable time, then interest charges will apply from 28 days after the amending law receives Royal Assent.
118. Where a proposed legislative change has been announced but not enacted and a taxpayer acts reasonably but still underestimates their income, interest would be remitted to the base rate provided the taxpayer lodges an amendment request within a reasonable time after the enactment of the new law.
Indirect taxes
119. Amendments to GST liabilities and other indirect tax liabilities are affected by subsection 105-85 of Schedule 1 of the TAA. This section essentially provides that indirect tax amending Acts cannot impose penalties or general interest charge earlier than 28 days after Royal Assent is given to the amending Act. This means that if a retrospective amendment to an indirect tax law increases liability to indirect tax, GIC in respect of the increased liability will only apply from 28 days after the amending Act receives Royal Assent.
Cases involving the use of the Commissioner's discretion to treat a particular document as a tax invoice or adjustment note
120. Where a recipient of a taxable supply does not hold a valid tax invoice in relation to the input tax credits claimed for a particular period, (or a valid adjustment note in relation to a claimed decreasing adjustment), and this is subsequently disclosed by audit or otherwise, a shortfall may result from any subsequent adjustment to the relevant activity statements. The resultant shortfall may also lead to the imposition of GIC.
121. Law Administration Practice Statement PS LA 2004/11 provides details of the policy in relation to the Commissioner's discretions to treat a particular document as a tax invoice or adjustment note and the circumstances when remission of the shortfall GIC may be appropriate.
Legislation
122. This section provides some further information on some the legislative provisions for imposition, notification and remission of shortfall interest charge and general interest charge.
Shortfall interest charge
123. The SIC provisions are contained in Division 280 of Schedule 1 to the TAA.
124. A taxpayer is liable to pay SIC on any additional amount of income tax payable as a result of an amended assessment for an income year (subsection 280-100(1) of Schedule 1 to the TAA).
125. The liability to SIC is for each day in the period:
- (a)
- beginning at the start of the day on which income tax under the first assessment for that income year was due to be paid, or would have been due to be paid if there had been any, and
- (b)
- ending at the end of the day before the day on which the Commissioner gave notice of the amended assessment (subsection 280-100(2) of Schedule 1 to the TAA).
126. However, if an amended assessment reinstates all, or part of, a particular item that had been reduced by an earlier amended assessment, the SIC calculation period for the reinstated liability starts from the due date of the earlier amended assessment. If the earlier amended assessment was a net credit, then the calculation starts from the day any tax would have been payable (subsection 280-100(3) of Schedule 1 to the TAA). This later start date is because the shortfall does not arise from an error in the original assessment, but from the taxpayer subsequently requesting an amendment that incorrectly reduces their liability.
127. The SIC rate for a day is worked out by adding three percentage points to the base interest rate for that day and dividing that total by the number of days in the calendar year (subsection 280-105(2) of Schedule 1 to the TAA). This has the effect of producing a SIC rate that reflects benchmark business borrowing rates.
128. For each day in a particular quarter of the year, the base interest rate equals the monthly average yield of 90 day Bank Accepted Bills for a prescribed previous month. For example, for the quarter 1 January to 31 March, the base interest rate is the monthly average yield of 90 day Bank Accepted Bills for the preceding November (subsection 8AAD(2) of the TAA).
129. The SIC is worked out daily on a compounding basis (subsection 280-105(1) of Schedule 1 to the TAA).
130. The Commissioner must give the taxpayer a notice stating the amount of the SIC liability. This amount can be included in another notice that the Commissioner gives to the taxpayer, such as the notice of amended assessment (subsections 280-110(1) and (2) of Schedule 1 to the TAA).
131. The SIC is due and payable 21 days from when notice of the amount of the charge is given to the taxpayer (subsection 5-10 of the ITAA 1997).
132. The Commissioner may remit all, or part of, an amount of SIC if the Commissioner considers it fair and reasonable to do so (subsection 280-160(1) of Schedule 1 to the TAA).
133. Without limiting the general remission power, in deciding whether to remit the Commissioner must have regard to:
- (i)
- the principle that remission should not occur just because the benefit received from the temporary use of the shortfall amount is less than the SIC, and
- (ii)
- the principle that remission should occur where the circumstances justify the Commonwealth bearing part or all of the cost of delayed payments (subsection 280-160(2) of Schedule 1 to the TAA).
134. If a remission request is made in the approved form, the Commissioner must give a written statement of the reasons for a decision not to remit an amount of SIC (section 280-165 of Schedule 1 to the TAA).
135. However if a remission request is not made in the approved form, it does not prevent the Commissioner from considering the request. Where this happens, the Commissioner will provide written reasons of the decision.
136. The content of a statement of reasons for a decision is provided in section 25D of the Acts Interpretation Act 1901. That section states '... the instrument giving the reasons shall also set out the findings on material questions of fact and refer to the evidence or other material on which those findings were based'.
137. A taxpayer may object using the provisions in Part IVC of the TAA against a decision of the Commissioner not to remit an amount of SIC where the amount not remitted is more than 20% of the additional amount of income tax on which it is calculated (section 280-170 of Schedule 1 to the TAA).
Example: SIC of $2,000 is payable in respect of a shortfall of $8,000. The Commissioner makes a decision not to remit any SIC. As the amount of SIC not remitted ($2,000) exceeds 20% of the shortfall ($2,000/$8,000 = 25%) then the taxpayer may object to the remission decision.
If the Commissioner had remitted $500 SIC so that $1,500 remained payable then the taxpayer would not be able to object to the decision as the SIC not remitted does not exceed 20% of the shortfall ($1,500/$8,000 = 18.75%)
138. The rights to a statement of reasons and the formal objection rights relating to decisions not to remit an amount of SIC are in addition to, and do not replace, existing rights under the Administrative Decisions (Judicial Review) Act 1977 (ADJR).
General interest charge
139. The legislative scheme for late payment GIC is in two parts. Liability to GIC is dealt with in various provisions in the tax laws. For example liability to GIC in respect of late payment of an income tax liability is provided at section 5-15 of the ITAA 1997. The second part of the scheme, which describes the basis for calculation of GIC, is set out in Division 1 of Part IIA of the TAA.
140. The liability to GIC for late payment is for each day in the period:
- (i)
- starting at the beginning of the day by which the tax was due to be paid, and
- (ii)
- finishing at the end of the last day on which, at the end of the day, any of the tax (or GIC on that tax) remains unpaid.
141. The GIC rate for a day is currently worked out by adding seven percentage points to the base interest rate for that day and dividing that total by the number of days in the calendar year (subsection 8AAD(1) of the TAA). This has the effect of producing a GIC rate that may be high (compared with indicator rates for commercial borrowing) for many taxpayers to encourage prompt payment of tax liabilities.
142. The base interest rate is the same as that used for SIC (see paragraph 127 of this practice statement).
143. GIC is worked out daily on a compounding basis (section 8AAC of the TAA).
144. There are no notification requirements for GIC, it being payable at the end of each day (section 8AAE of the TAA).
145. The Commissioner may remit all, or part of, GIC (section 8AAG of the TAA). However, remission can only be made if circumstances set out in the law are met (subsections 8AAG(2) to (5) of the TAA). These include special circumstances where it is fair and reasonable to remit.
146. When notifying a decision not to remit GIC, the Commissioner will provide the reasons for the decision.
147. While a taxpayer can, in some circumstances, object against a decision not to remit SIC, there are no objection rights under the taxation law against a remission decision relating to GIC. A taxpayer can seek formal review of remission decisions under the ADJR.
148. This practice statement only deals with remission of GIC that accrues during the shortfall period and needs to be read in conjunction with the chapter entitled 'General Interest Charge' in the ATO Receivables Policy, which details the policy for remission of GIC in other circumstances.
Diagram of interest charges and shortfall periods
149. Below is a diagram illustrating when interest charges accrue in shortfall periods.
Amendment history
| Date of amendment | Part | Comment |
|---|---|---|
| 11 July 2012 | Generally | Updated to current ATO publication style. |
| Paragraph 12 | Update table to recognise that SIC also applies to MRRT and PRRT | |
| New paragraph 13 | This confirms that a consistent approach with income tax will be taken to administering SIC for both MRRT and PRRT. Also paragraph references have been updated to accommodate this new paragraph. | |
| New paragraph 104 (previously 103) | Updated to recognise that rulings can be issued for MRRT. | |
| 26 August 2010 | Paragraph 103 | Dot points inserted for additional taxes that section 357-55 of Schedule 1 to the TAA may apply to. |
| 1 July 2010 | Paragraph 12, 133, 141 | Updated legislative references (Part VI of the ITAA 1936 rewrite). |
| 5 May 2008 | Paragraphs 119 to 121 (including heading)Paragraph 5 and references | Deleted. |
| 26 Sept 2006 | Paragraph 17 | Change to the definition of 'commencement of audit'. |
| Paragraph 18 | Clarification of definition of 'completion of audit'. | |
| Paragraph 22 | Clarification of definition of 'shortfall amount'. | |
| Paragraph 24 | Clarification of definition of 'shorfall period'. | |
| Paragraph 53 | Second example clarified. | |
| Paragraph 74 | Change to date the auditor phones in the Example. | |
| Paragraph 84 | Words 'the notification of' added to second dot point. | |
| Paragraph 103 | Extra dot point regarding net fuel amount etc added. | |
| Paragraph 118 | Heading and section reference updated. |
Date of Issue: 1 August 2006
Date of Effect: 1 July 2005
The relevant rate for a period can be accessed at http://www.ato.gov.au/Rates/Shortfall-interest-charge-(SIC)-rates/
The relevant rate for a period can be accessed at http://www.ato.gov.au/Rates/Shortfall-interest-charge-(SIC)-rates/
There will be some circumstances when notification will not be appropriate, for example where it is suspected a case involves fraud or evasion or other criminal activity.
These service standards are detailed in Taxpayers' Charter, Explanatory Booklet '03 - Our Service Standards'.
Where a shortfall amount is subject to shortfall GIC, GIC would stop accruing upon payment of the shortfall because the shortfall amount has a due and payable date that is in the past rather than the future.
File 06/12257
Related Practice Statements:
Law Administration Practice Statement PS LA 2003/2
Law Administration Practice Statement PS LA 2004/5(GA)
Law Administration Practice Statement PS LA 2004/11
Other References:
Receivables Management Policy
Subject References:
general interest charge
Report on Aspects of Income Tax Self Assessment (August 2004)
shortfall interest charge
Legislative References:
Administrative Decisions (Judicial Review) Act 1977
Acts Interpretation Act 1901 25D
FBTAA 1986 93
ITAA 1936 170AA
ITAA 1936 214A
ITAA 1997 5-1
ITAA 1997 5-10
ITAA 1997 5-15
ITAA 1997 701-70
Product Grants and Benefits Administration Act 2000 8
TAA 1953 Pt IIA Div 1
TAA 1953 8AAC
TAA 1953 8AAD(1)
TAA 1953 8AAD(2)
TAA 1953 8AAE
TAA 1953 8AAG
TAA 1953 8AAG(2)
TAA 1953 8AAG(3)
TAA 1953 8AAG(4)
TAA 1953 8AAG(5)
TAA 1953 Pt IVC
TAA 1953 40
TAA 1953 46A
TAA 1953 Sch 1 16-80
TAA 1953 Sch 1 Div 280
TAA 1953 Sch 1 280-105(1)
TAA 1953 Sch 1 280-105(2)
TAA 1953 Sch 1 280-100(1)
TAA 1953 Sch 1 280-100(2)
TAA 1953 Sch 1 280-100(3)
TAA 1953 Sch 1 280-110(1)
TAA 1953 Sch 1 280-110(2)
TAA 1953 Sch 1 280-160(1)
TAA 1953 Sch 1 280-160(2)
TAA 1953 Sch 1 280-160(2)(b)
TAA 1953 Sch 1 280-165
TAA 1953 Sch 1 280-170
TAA 1953 Sch 1 284-75
TAA 1953 Sch 1 357-55
TAA 1953 Sch 1 361-5
TAA 1953 Sch 1 361-5(1)
TAA 1953 Sch 1 361-5(2)
Taxation (Interest on Overpayments and Early Payments) Act 1983 Pt IIA
| Contact email | OperationalPolicyAssuranceandLawWorkManagement@ato.gov.au |
| Section | Operational Policy, Assurance and Law |
| Date: | Version: | ||
| 5 May 2008 | Updated statement | ||
| 1 July 2010 | Updated statement | ||
| 26 August 2010 | Updated statement | ||
| You are here | 11 July 2012 | Updated statement | |
| 19 June 2014 | Updated statement | ||
| 28 August 2014 | Updated statement | ||
| 10 December 2015 | Updated statement | ||
| 30 October 2019 | Updated statement | ||
| This practice statement was originally published on 1 August 2006. Versions published from 5 May 2008 are available electronically - refer to the online version of the practice statement. Versions published prior to this date are not available electronically. If needed, these can be requested by emailing TCNLawPublishingandPolicy@ato.gov.au. | |||
Copyright notice
© Australian Taxation Office for the Commonwealth of Australia
You are free to copy, adapt, modify, transmit and distribute material on this website as you wish (but not in any way that suggests the ATO or the Commonwealth endorses you or any of your services or products).
